TÌM ĐIỂM ĐỐI XỨNG QUA MẶT PHẲNG

Phép trở nên hình F trong không khí là một quy tắc để với từng điểm M (trong ko gian), xác minh được một điểm M’duy nhất call là hình ảnh của điểm M qua phép biến chuyển hình F. Ta còn nói F đổi thay điểm M thành điểm M’và kí hiệu M’= F(M).

Bạn đang xem: Tìm điểm đối xứng qua mặt phẳng

Qua phép biến đổi hình F, mỗi hìnhđược trở thành hình’gồm toàn bộ các hình ảnh của các điểm trực thuộc hình.

Sau phía trên ta xét phép đối xứng qua mặt phẳng, đó là một phép trở nên hình thường xuyên gặp.1. Phép đối xứng qua phương diện phẳng

ĐỊNH NGHĨA 1 (h.7)

Phép đối xứng qua mặt phẳng(P) là phép đổi mới hình trở nên mỗi điểm thuộc (P) thành chính nó và thay đổi mỗi điểm M không thuộc (P) thành điểm M’sao cho (P) là mặt phẳng trung trực của đoạn thẳng MM’.

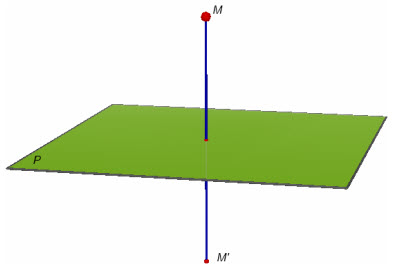
Hình 7

Nếu phép đối xứng qua mp(P) đổi thay hai điểm M, N theo lần lượt thành nhì điển M’, N’thì M’N’= MN. (Như vậy nói cách khác : phép đối xứng qua mặt phẳng là phép trở nên hình bảo toàn khoảng cách giữa hai điểm bất kì).

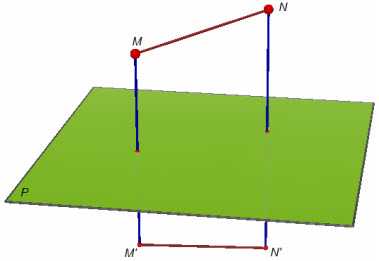
Hình 8

1(để chứng minh định lí 1)

NếuM, Nnằn trên (P) thìM’vàN’trùngMvàN’trùngNnênM’N’=MN.

Nếu có ít nhất 1 trong các hai điểmM, Nkhông nằm trong (P) thì bao gồm mp(Q) đi qua những điểmM, N, M’, N’.Hãy dùng kỹ năng và kiến thức hình học tập phẳng để triệu chứng minhM’N’=MN.

Khi đứng trước một tấm gương phẳng, mỗi cá nhân sẽ nhận thấy hình của bản thân ở “phía sau” tấm gương kia (h.9). Phép đối xứng qua phương diện phẳng của tấm gương sẽ “biến” mọi người thành hình của họ.

Hình 9.Ảnh chụp một em bé nhỏ trước gương

Hình 10 là hình ảnh của Tháp Rùa đã soi bóng trên mặt nước hồ hoàn kiếm (Hà Nội). Mặt hồ nước xem như là 1 phần của khía cạnh phẳng, phép đối xứng qua mặt phẳng đó đổi thay Tháp Rùa thành chiếc bóng của nó.

Hình 10.Ảnh chụp Tháp Rùa và bóng của nó

2. Khía cạnh phẳng đối xứng của một hình

ĐỊNH NGHĨA 2

Nếu phép đối xứng qua khía cạnh phẳng (P) biến hìnhthành chủ yếu nó thì (P) hotline làmặt phẳng đối xứngcủa hình.Một số ví dụVí dụ 1

Mọi phương diện phẳng đi qua tâm của mặt cầu đông đảo là phương diện phẳng đối xứng của mặt ước (h.11).

Hình 11

Ví dụ 2

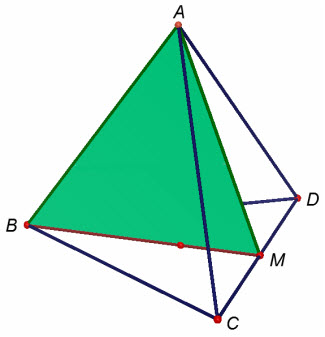
Cho tứ diện gần như ABCD (h.12). điện thoại tư vấn M là trung điểm của cạnh CD thì phép đối xứng qua mp(ABM) biến chuyển A thành A, B thành B, C thành D, D thành C. Như vậy, phép đối xứng đó biến tứ diện ABCD thành bao gồm nó, suy ra mặt phẳng (ABM) thành khía cạnh phẳng đối xứng của tứ diện ABCD.

Hình tứ diện mọi ABCD gồm sáu mặt phẳng đối xứng. Đó là những mặt phẳng đi sang một cạnh với trung điểm của cạnh đối diện.

Hình 12

Ví dụ 3

Xét hình lập phương ABCD.A’B’C’D’(h.13).

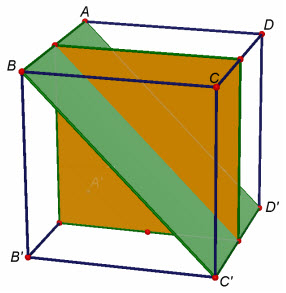
Hình 13

Nếu (P) là mặt phẳng trung trực của cạnh AB thì nó cũng chính là mặt phẳng trung trực của cạnh AB thì nó cũng là mặt phẳng trung trực của những cạnh CD, A’B’và C’D’, bởi thế nó là phương diện phẳng đối xứng của hình lập phương. Tương tự, các mặt phẳng trung trực của các cạnh AD, cùng AA’cũng là hầu hết mặt phẳng đối xứng của hình lập phương.

Gọi (Q) là mặt phẳng đi qua hai cạnh đối diện AB và C’D’thì (Q) là phương diện phẳng đối xứng của hình lập phương vì chưng phép đối xứng qua (Q) trở thành mỗi điểm A, B, C’, D’thành chủ yếu nó và thay đổi điểm A’thành D, D thành A’,C thành B’và B’thành C.

?1Như vậy hình lập phương bao gồm bao nhiêu phương diện phẳngđối xứng ?3. Hình bát diện phần lớn và phương diện phẳng đối xứng của nóHình 14 là 1 trong những hình đa diện bao gồm 8 mặt là các tam giác các :EAB, EBC, ECD, EDA, FAB, FBC, FCDvàFDA,có 6 đỉnhA, B, C, D, E, F, mỗi đỉnh là đỉnh phổ biến cho 4 tam giácđều. Hình đó điện thoại tư vấn làhình chén bát diện đều(hayhình tám khía cạnh đều) và được kí hiệu làABCDEF.

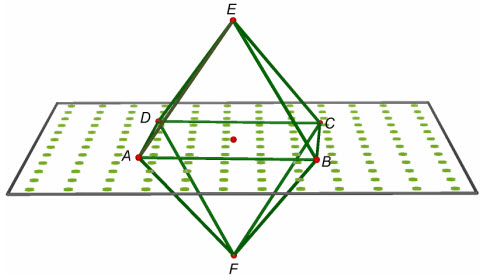
Hình 14

Tính chất

Bốn đỉnh A, B, C, D nằm trong một phương diện phẳng và đó là 1 mặt phẳng đối xứng của hình bát diện đầy đủ ABCDEF.Chứng minh

Vì mỗi điểmA, B, C, Dcách đầy đủ hai điểmEvàFnên chúng nằm trên mặt phẳng trung trực của đoạn thẳngEF. Phép đối xứng qua mặt phẳng đó biến mỗi điểmA, B, C, Dthành chủ yếu nó và biến đổi điểmEthànhF,FthànhEnên mp(ABCD) là phương diện phẳng đối xứng của chén bát diện đềuABCDEF.¢

2Tìm thêm các mặt phẳng đối xứng không giống của hình chén bát diện đều.4. Phép dời hình và sự bởi nhau của những hìnhPhép dời hình trong không khí được định nghĩa tương tự như trong phương diện phẳng.Định nghĩa phép dời hình

Một phép phát triển thành hình F trong không khí được call làphép dời hìnhnếu nó bảo toàn khoảng cách giữa hai điểm bất kỳ (có nghĩa là ví như F vươn lên là hai điểm bất kể M, N theo lần lượt thành nhì điểm M’, N’thì M’N’=MN).Từ định nghĩa đó, ta suy ra phép dời hình biến hóa đường trực tiếp thành con đường thẳng, phương diện phẳng thành mặt phẳng,… .Hiển nhiên phép đối xứng qua khía cạnh phẳng là 1 trong phép dời hình.Phép đồng nhất(biến mỗi điểm thành bao gồm nó) là một phép dời hình.Rõ ràng trường hợp thực hiện thường xuyên các phép dời hình thì ta cũng có tác dụng là phép dời hình. Có thể nói :Hợp thành của những phép dời hình là phép dời hình.Một số lấy một ví dụ về phép dời hìnhNgoài phép đối xứng quanh phương diện phẳng, ta thường chạm mặt một số phép dời hình dưới đây :

•Phép tịnh tiến: Phép tịnh tiến theo vectơ

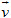
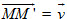
là phép đổi mới hình biến mỗi điểmMthành điểmM’sao cho

•Phép đối xứng qua mặt đường thẳng(còn điện thoại tư vấn làphép đối xứng trục) : cho đường thẳngd, phép đối xứng qua mặt đường thẳngdlà phép thay đổi hình biến mỗi điểm thuộcdthành chính nó và thay đổi mỗi điểmMkhông thuộcdthành điểmM’sao cho trong mặt phẳng (M, d),dlà mặt đường trung trực của đoạn thẳngMM’.

•Phép đối xứng sang một điểm(còn call làphép đối xứng tâm) : mang đến điểmO, phép đối xứng qua điểmOlà phép trở thành hình biến đổi mỗi điểmMthành điểmM’sao cho

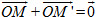
Xem thêm: Hộp Kiểm Tra Điện Trở Đất - Hộp Kiểm Tra Điện Trở Tiếp Địa 210X160X100

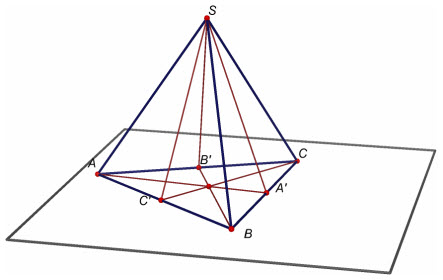
Định nghĩa nhì hình bằng nhau

Hai hìnhvà’gọi làbằng nhaunếu bao gồm một phép dời hình biến đổi hình này thành các hình kia.?2Hai mặt mong có nửa đường kính bằng nhau thì có bởi nhau hay không ? do sao ?Ví dụ 4.Cho hình chóp tam giác phần lớn S.ABC. Call A’, B’, C’lần lượt là trung điểm của cạnh BC, CA và AB. Khi đó hai tứ diện SABA’và SBCB’bằng nhau.Giải(h.15)

Hình 15

Thật vậy, phép đối xứng qua mp(SAA’) biến các điểmS, A, B, A’lần lượt thành những điểmS, A, C, A’và phép đối xứng qua mp(SCC’) biến những điểmS, A, C, A’lần lượt thành các điểmS, B, C, B’. Như vậy, qua nhị phép đối xứng trên, bốn đỉnhS, A, B, A’của tứ diệnSABA’biến thành bốn đỉnhS, B, C, B’của tứ diệnSBCB’nêu theo định nghĩa, nhị tứ diện đó bằng nhau. ¢ĐỊNH LÍ 2

Hai hình tứ diện ABCD với A’B’C’D’bằng nhau nếu bọn chúng có các cạnh tương xứng bằng nhau, nghĩa là AB=A’B’, BC=B’C’, CD=C’D’, AC=A’C’, BD=B’D’.Chứng minh.Ta xét các trường hòa hợp sau :

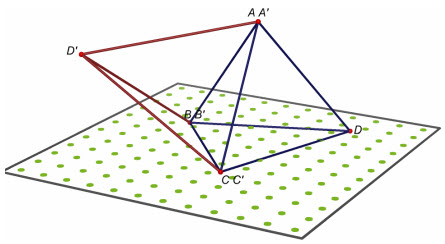
Trường thích hợp 1(h.16).Hai hình tứ diện có cha cặp đỉnh khớp ứng trùng nhau,chẳng hạnAtrùngA’, BtrùngB’, CtrùngC’, DkhácD’.

Hình 16

Khi đó, từng điểmA, B, Ccách những hai điểmDvàD’trên mp(ABC) là phương diện phẳng trung trực của đoạn thẳngDD’,suy ra phép đối xứng qua mp(ABC) biến các đỉnhA, B, C, Dlần lượt thành các đỉnhA’, B’, C’, D’.Vậy hai tứ diệnABCDvàA’B’C’D’bằng nhau.

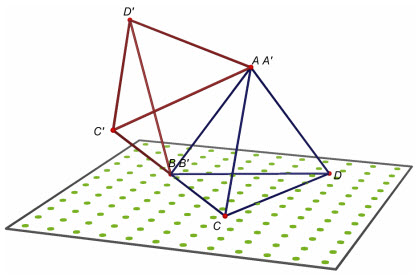
Trường phù hợp 2(h.17). Hai hình tứ diện đó có hai cặp đỉnh tương xứng trùng nhau,chẳng hạnAtrùngA’, BtrùngB’.

Hình 17

Khi đó gọi (P) là mặt phẳng trung trực của đoạn thẳngCC’thì (P) đi quaAvàB(vìAvàBcùng bí quyết đều nhì điểmCvàC’). Vậy phép đối xứng qua mp(P) sẽ phát triển thành cá điểmA, B, C, Dlần lượt thành những điểmA’, B’, C’, D1và cho nên vì vậy tứ diệnABCDbằng tứ diệnA’B’C’D1.

Vì nhị tứ diệnA’B’C’D1vàA’B’C’D’có các cạnh khớp ứng bằng nhau với có cha đỉnh khớp ứng trùng nhau yêu cầu theo trường hòa hợp 1, chúng bởi nhau.

Trường phù hợp 3. Hai hình tứ diện có một cặp đỉnh tương ứng trùng nhau,chẳng hạnAtrùngA’.

Khi đó, gọi (Q) là phương diện phẳng trung trực củaBB’thì (Q) đi quaA(vìAcách đềuBvàB’). Vậy phép đối xứng qua (Q) biến các điểmA, B, C, Dlần lượt thành những điểmA’, B’, C1, D1và vị đó, hai tứ diệnABCDvàA’B’C1D1bằng nhau. Mặt khác, nhì tứ diệnA’B’C1D1vàA’B’C’D’có những cạnh khớp ứng bằng nhau và có hai cặp đỉnh khớp ứng trùng nhau nên theo trường đúng theo 2, chúng bởi nhau.

Trường phù hợp 4. Hai hình tứ diện đó không tồn tại cặp đỉnh tương ứng nào trùng nhau.

Khi đó hotline (R) là khía cạnh phẳng trung trực củaAA’, phép đối xứng qua (R) biến các điểmA, B, C, Dlần lượt thành các điểmA’, B1, C1, D1nên tứ diệnABCDbằng tứ diệnA’B1C1D1: nhưng mà hai tứ diệnA’B1C1D1vàA’B’C’D’có cạnh tương ứng bằng nhau với một cặp đỉnh tương xứng trùng nhau, cho nên vì vậy chúng đều nhau theo trường hợp 3. ¢HỆ QUẢ 1

Hai tứ diện đều phải sở hữu cạnh đều nhau thì bởi nhau.

HỆ QUẢ 2

Hai hình lập phương gồm cạnh bằng nhau thì bởi nhau.Chứng minh(h.18)

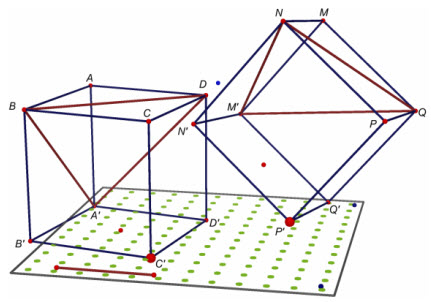
Hình 18

Giả sửABCD. A’B’C’D’vàMNPQ.M’N’P’Q’là nhì hình lập phương tất cả cạnh hầu như bằnga. Hai tứ diệnABDA’vàMNQM’có các cạnh khớp ứng bằng nhau nên bằng nhau, có nghĩa là có phép dời hìnhFbiến những điểmA, B, D, A’lần lượt thànhM, N, Q, M’. VìFlà phép dời hình nênFbiến hình vuông thành hình vuông, bởi vì đóFbiến các điểmCthành điểmP, biến hóa điểmB’thànhN’,biến điểmD’thànhQ’và biến những điểmC’thànhP’.Như vậy, nhị hình lập phương sẽ cho bằng nhau. ¢

Câu hỏi và bài xích tập

6.GọiĐlà phép đối xứng qua khía cạnh phẳng (P) vàalà một đường thẳng nào đó. Giả sửĐbiến đổi đường thẳngathành đường thẳnga’. Vào trường hợp nào thì :

a)atrùng vớia’;

b)asong songa’;

c)acắta’;

d)avàa’chéo nhau ?7.Tìm các mặt phẳng đối xứng của những hình sau đây :

a) Hình chóp tứ giác đầy đủ ;

b) Hình chóp cụt tam giác đông đảo ;

c) Hình vỏ hộp chữ nhật mà lại không xuất hiện nào là hình vuông.8.Cho hình lập phươngABCD. A’B’C’D’.Chứng minh rằng :

a) các hình chópA. A’B’C’D’vàC’.ABCDbằng nhau.

b) những hình lăng trụABC.A’B’C’vàAA’D’.BB’C’bằng nhau.9.Chứng minh rằng các phép tịnh tiến, đối xứng trục, đối xứng tâm là đều phép dời hình.10.Chứng minh rằng :

a) đúng theo thành của nhị phép đối xứng qua hai mặt phẳng tuy vậy song (P) cùng (Q) là một trong những phép tịnh tiến ;

b) thích hợp thành của nhì phéo đối xứng qua hai mặt phẳng (P) và (Q)vuông góc với nhau là 1 trong những phép đối xứng qua mặt đường thẳng.