Giải bài tập hình học 11 nâng cao chương 2

Giải bài tập trang 67, 68 bài xích 4 hai mặt phẳng tuy vậy song SGK Hình học 11 Nâng cao. Câu 29: trong số mệnh đề sau, mệnh đề làm sao đúng ...

Bạn đang xem: Giải bài tập hình học 11 nâng cao chương 2

Câu 29 trang 67 SGK Hình học tập 11 nâng cao

Trong những mệnh đề sau, mệnh đề nào đúng ?

a. Hai mặt phẳng phân biệt cùng tuy vậy song với một đường thẳng thì tuy vậy song với nhau

b. Nhì mặt phẳng biệt lập cùng song song cùng với một mặt phẳng thì tuy nhiên song với nhau

c. Trường hợp hai phương diện phẳng song song thì phần lớn đường thẳng nằm ở một phương diện phẳng đều song song với phương diện phẳng còn lại.

d. Trường hợp hai phương diện phẳng tuy nhiên song thì mỗi con đường thẳng nằm tại một mặt phẳng này đều song song với đa số đường thẳng nằm trên mặt phẳng kia.

e. Giả dụ hai phương diện phẳng minh bạch lần lượt trải qua hai mặt đường thẳng tuy vậy song thì song song với nhau.

f. Trường hợp một con đường thẳng cắt một trong những hai khía cạnh phẳng tuy vậy song thì giảm mặt phẳng còn lại.

Giải

a. Sai vì chưng hai mặt phẳng có thể cắt nhau theo giao tuyến tuy nhiên song với con đường thẳng vẫn cho.

b. Đúng

c. Đúng

d. Sai

e. Sai vì rất có thể hai khía cạnh phẳng giảm nhau.

f. Đúng

Câu 30 trang 67 SGK Hình học 11 Nâng cao

Trong những mệnh đề sau, mệnh đề nào đúng?

a. Hình hộp là một trong hình lăng trụ

b. Hình lăng trụ có toàn bộ các cạnh tuy nhiên song

c. Hình lăng trụ có toàn bộ các khía cạnh bên bằng nhau

d. Hình lăng trụ có những mặt bên là hình bình hành

e. Hình vỏ hộp có các mặt đối diện bằng nhau

Giải

a. Đúng

b. Sai vì chưng cạnh lòng không tuy vậy song cùng với cạnh bên.

c. Sai

d. Đúng

e. Đúng

Câu 31 trang 68 SGK Hình học tập 11 cải thiện

Cho hai tuyến đường thẳng chéo nhau. Chứng minh rằng tất cả đúng hai mặt phẳng tuy vậy song với nhau lần lượt trải qua hai đường thẳng đó

Giải

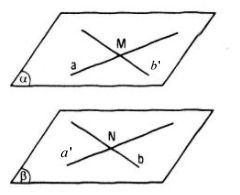
Gọi hai tuyến đường thẳng chéo nhau là a và b.

Trên mặt đường thẳng a, ta đem điểm M, qua M kẻ mặt đường thẳng b’ // b

Trên đường thẳng b, ta rước điểm N, qua N ta kẻ đường thẳng a’ // a

Gọi (α) = mp(a, b’), (β) = mp(b, a’) thì (α) // (β)

* Ta minh chứng cặp khía cạnh phẳng (α), (β) là duy nhất.

Thật vậy, giả sử sống thọ cặp (α’) , (β’) làm sao cho (α’) chứa a, (β’) đựng b với ((α’) // (β’)). Ta chứng tỏ ((α’) ≡ (α)) cùng ((β’) ≡ (β)) .

- bởi (α’) cùng (α) cùng chứa a, yêu cầu nếu (α’) với (α) ko trùng nhau thì ((α’) ∩ (α) = a) (1)

- bởi vì ( (α’) // (β’) ⇒ b // (α’)) (2)

- vày ((α) // (β) ⇒ b // (α)) (3)

Từ (1), (2) với (3) suy ra a // b, mâu thuẫn giả thiết

Vậy ((α) ≡ (α’)), giống như ((β) ≡ (β’))

Do đó cặp khía cạnh phẳng ((α), (β)) duy nhất.

Câu 32 trang 68 SGK Hình học tập 11 nâng cấp

Cho hai đường thẳng chéo cánh nhau a và b lần lượt nằm trên hai mặt phẳng tuy nhiên song (P) và (Q). Chứng minh rằng ví như điểm M không nằm bên trên (P) với không nằm trên (Q) thì gồm duy độc nhất một mặt đường thẳng đi qua M giảm cả a và b

Giải

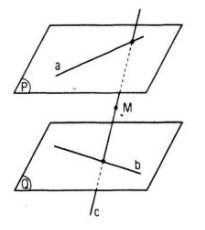
Giả sử c = mp ( M, a) ∩ mp(M, b). Ta cần chứng tỏ c giảm cả a và b.

Vì c với a cũng vị trí một khía cạnh phẳng và thiết yếu trùng nhau ( bởi vì c qua M cùng a không đi qua M) cần hoặc c // a hoặc c cắt a. Cũng vậy, hoặc c // b hoặc c giảm b.

Không thể xảy ra đồng thời c // a; c // b do a cùng b chéo cánh nhau. Vậy nếu như c tuy vậy song với a và c bắt buộc cắt b, tức là c qua một điểm của mp (Q) và tuy vậy song cùng với a, suy ra c bắt buộc thuộc mp (Q), và vì vậy M ở trong (Q) (trái mang thiết).

Tương tự, ko thể tất cả c song song với b.

Tóm lại c giảm a cùng b.

Nếu còn tồn tại đường trực tiếp c’ khác c trải qua M, cắt cả a cùng b thì a với b đồng phẳng. Vô lí.

Câu 33 trang 68 SGK Hình học tập 11 nâng cấp

Trong mặt phẳng (P) mang đến hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ tứ đường trực tiếp a, b, c, d song một tuy nhiên song với nhau cùng không vị trí (P). Một phương diện phẳng cắt a, b, c, d theo lần lượt tại tư điểm A’, B’, C’, D’. Chứng minh rằng A’B’C’D’ là hình bình hành

Giải

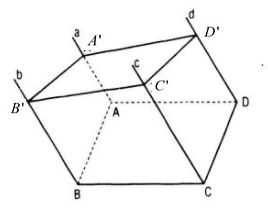
Ta có: (left{ matrix a//b cr AD//BC cr a cap AD=A cr ight.Rightarrow left( a,d ight)//left( b,c ight) )

Tương trường đoản cú (a, b) // (c, d).

Vì nhì mặt phẳng (a, b) với (c, d) tuy nhiên song nhau bắt buộc mp(A’B’C’) cắt hai mặt phẳng này

lần lượt theo nhị giao đường A’B’ cùng C’D’ song song nhau.

Tương từ A’D’// B’C’.

Vậy A’B’C’D’ là hình bình hành.

Câu 34 trang 68 SGK Hình học 11 nâng cấp

Cho tứ diện ABCD. Gọi M là trung điểm của AB. Hỏi khía cạnh phẳng (P) qua điểm M, song song với tất cả AD cùng BC có đi qua trung điểm N của CD không ? lý do ?

Giải:

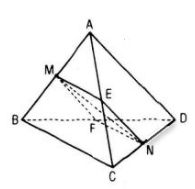
Giả sử (P) cắt BD, AC với CD thứu tự tại F, E, N. Vì AD // (P) phải (P) giảm mp(ABD) theo giao con đường MF // AD.

Vì M là trung điểm của AB phải F là trung điểm của BD.

Vì BC // (P) phải (P) cắt mp(BCD) theo giao tuyến đường FN // BC. Vì F là trung điểm của BD bắt buộc N là trung điểm của CD.

Câu 35 trang 68 SGK Hình học tập 11 nâng cao

Cho hai điểm M, N lần lượt biến đổi trên hai mặt phẳng song song (P) và (Q). Search tập hợp những điểm I nằm trong đoạn thẳng MN thế nào cho (IM over IN = k,k e 0)cho trước

Giải

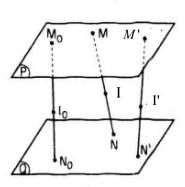
Thuận. đưa sử M (in) (P), N (in) (Q) và điểm I ở trong đoạn thẳng MN thế nào cho (IM over IN = k.)

Trên nhì mặt phẳng (P) với (Q), ta lần lượt đem hai điểm thắt chặt và cố định M0 cùng N0 rồi mang một điểm I0 thuộc đoạn trực tiếp M0N0 làm thế nào để cho (M_0I_0 over N_0I_0 = k.) lúc ấy điểm I0 cố kỉnh định.

Ta có: (IM over IN = I_0M_0 over I_0N_0left( = k ight))

(Rightarrow IM over I_0M_0 = IN over I_0N_0 = IM + IN over I_0M_0 + I_0N_0 = MN over M_0N_0)

Áp dụng định lí Ta-lét đảo, ta suy đi ra ngoài đường thẳng I0I thuộc một mặt phẳng (R) song song cùng với (P) với (Q). Mặt phẳng (R) cố định vì nó qua điểm thắt chặt và cố định I­0 và tuy nhiên song với khía cạnh phẳng thắt chặt và cố định (P). Vậy điểm I thuộc mặt phẳng (R) thay định.

Xem thêm: Top 20 Món Ăn Ngon Và Các Món Ăn Dễ Làm Trong Ngày Giãn Cách

Đảo. Ngược lại, mang một điểm I’ bất cứ trên phương diện phẳng (R). Qua I’ ta kẻ một mặt đường thẳng giảm hai mặt phẳng (P) và (Q) lần lượt tại M’ cùng N’. Xét hai mèo tuyến M0N0 , M’N’ và tía mặt phẳng tuy vậy song (P), (Q), (R).

Theo định lí Ta-lét ta có: (I"M" over I_0M_0 = I"N" over I_0N_0 = M"N" over M_0N_0)

Từ đó, ta suy ra I trực thuộc đoạn thẳng M’N’ cùng (I"M" over I"N" = I_0M_0 over I_0N_0 = k)

Kết luận: Tập hợp điểm I ở trong đoạn trực tiếp MN sao để cho (IM over IN = k) là mặt phẳng (R) nói trên.

Câu 36 trang 68 SGK Hình học tập 11 nâng cấp

Cho hình lăng trụ đứng tam giác ABC.A’B’C’. Gọi H là trung điểm của cạnh A’B’.

a. Minh chứng rằng con đường thẳng CB’ song song với mp(AHC’)

b. Search giao đường d của hai mặt phẳng (AB’C’) và (A’BC). Minh chứng rằng d tuy vậy song cùng với mp(BB’C’C)

c. Xác định thiết diện của hình lăng trụ ABC.A’B’C’ lúc cắt vì mp(H , d)

Giải

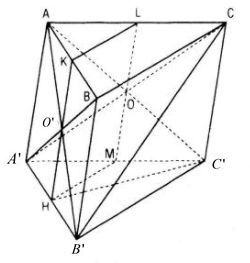
a) chứng minh CB" // (AHC’)

Ta tìm trong (AHC’) một con đường thẳng tuy vậy song cùng với CB’, ước ao vậy ta tìm giao tuyến của một phương diện phẳng chứa CB’ cùng với (AHC’), chính là (A’CB’).

Gọi O là giao điểm AC’ cùng A’C.

AA’C’C là hình bình hành phải O là trung điểm của A’C.

Do đó HO là mặt đường trung bình của ∆A’B’C

⇒ HO // B’C ⇒ B’C // (AHC’). ( vày HO (subset) (AHC’)).

b) search giao đường d của (AB’C’) và (A’BC).

Gọi O’ là giao điểm của AB’ với A’B thì O, O’ là nhị điểm chung của nhì mặt phẳng (AB’C’) cùng (A’BC) buộc phải (AB’C’) ∩ (A’BC) = OO’

Vậy d = OO’. Ta tất cả O’ là trung điểm của AB’ ( vày AA’B’B là hình bình hành).

⇒ OO’ là đường trung bình của ∆AB’C’.

⇒ OO’ // B’C" // BC ⇒ OO’ // (BB’C’C) ⇒ d // (BB’C’C)

c) hotline K = HO’ ∩ AB thì HK // AA’

Qua O kẻ ML // AA’ ( M ∈ A’C’, L ∈ AC).

Thiết diện bắt buộc tìm là hình bình hành HKLM.

Câu 37 trang 68 SGK Hình học 11 nâng cấp

Cho hình vỏ hộp ABCD.A’B’C’D’. Minh chứng rẳng

a. Mp(BDA’) // mp(B’D’C)

b.Đường chéo AC’ đi qua những trọng trung khu G1, G2 của hai tam giác BDA’ với B’D’C

c. G1 cùng G2 phân tách đoạn AC’ thành tía phần bởi nhau

d. Các trung điểm của sáu cạnh BC, CD, DD’, D’A’, A’B’,B’B cùng nằm bên trên một mặt phẳng

Giải:

a) chứng minh ( BDA’) // (B’D’C)

Ta tất cả tứ giác BB’D’D với A’B’CD là những hình bình hành bắt buộc : BD // B’D’ và DA’ // B’C

⇒ hai mặt phẳng (BDA’) cùng (B’D’C) có các cặp mặt đường thẳng cắt nhau và tuy vậy song nhau từng đôi một buộc phải chúng song song.

Vậy (BDA’) // (B’D’C).

b) chứng minh G1 , G2 ∈ AC’

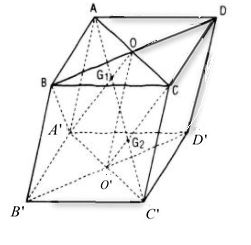
Gọi O, O’ theo thứ tự là trung khu của hình bình hành ABCD và A’B’C’D’.

Trong khía cạnh phẳng (AA’C’C) gọi G1 , G2 theo thứ tự là giao điểm của AC’ cùng với A’O với O’C. Ta chứng minh G1, G2 lần lượt là trong trái tim của ∆A’BD và ∆CB’D’.

Thật vậy, ta bao gồm ∆G1OA đồng dạng ∆G1A’C’ ( do AC // A’C’)

( Rightarrow G_1O over G_1A" = OA over A"C" = 1 over 2 Rightarrow A"G_1 over A"O = 2 over 3)

⇒ G1 là giữa trung tâm ∆A’BD.

Tương tự, G2 là trung tâm ∆CB’D’. Vậy AC’ đi qua G1, G2 .

c) chứng tỏ AG1 = G1G2 = G2C’

Theo câu trên , ta có:

(AG_1 over G_1C" = AO over A"C" = 1 over 2) ( vì ∆G1OA đồng dạng ∆G1A’C’) ( Rightarrow AG_1 = 1 over 3AC") (1)

Tương tự: (C"G_2 over G_2A = C"O" over CA = 1 over 2) ( vị ∆G2C’O" đồng dạng ∆G2AC) ( Rightarrow C"G_2 = 1 over 3AC") (2)

Từ (1) và (2) suy ra: AG1 = G1G2 = G2C’.

d)

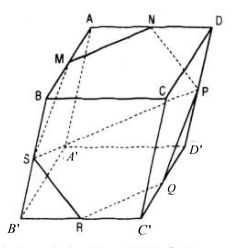
Gọi M, N, P, Q, S, R theo lần lượt là trung điểm của các cạnh AB, AD, DD’, C’D’, C’B’, B’B.

Ta có: (left{ matrix MN//BD cr SP//BD cr ight. Rightarrow MN//SP)

Gọi (α) = (MN, SP)

Ta tất cả : (left{ matrix PQ//DC" cr MS//AB" cr ight. Rightarrow PQ//MS)

( vày DC’ // AB’)

⇒ PQ ⊂ (α) cho nên Q ∈ (α).

Tương tự: QR // MN ⇒ QR ⊂ (α) vì thế R ∈ (α).

Vậy M, N, P, Q, R, S ∈ (α).

Mặt khác bởi (left{ matrix MS//AB" cr NP//AD" cr ight.) đề nghị (MNPQRS) // (AB’D").

Câu 38 trang 68 SGK Hình học 11 nâng cao

Chứng minh rẳng tổng bình phương toàn bộ các đường chéo cánh của một hình hộp bằng tổng bình

phương toàn bộ các cạnh của hình vỏ hộp đó

Giải

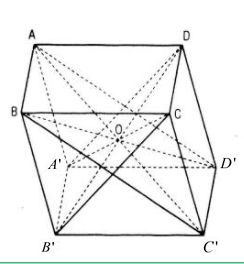
Áp dụng tính chất: “ vào một hình bình hành, tổng bình phương nhì đường chéo bằng tổng bình phương tư cạnh.”

Đặt AB = a, BC = b, AA’ = c ( chính là 3 size của hình hộp).

Trong hình bình hành ABC’D’ ta có:

(AC"^2 + BD"^2 = 2left( a^2 + BC"^2 ight)) (1)

Trong hình bình hành A’B’CD ta có:

(A"C^2 + B"D^2 = 2left( a^2 + B"C^2 ight)) (2)

Cộng (1) và (2) ta được :

 (AC"^2 + BD"^2+A"C^2 + B"D^2 = 2left( 2a^2 + BC"^2 + B"C^2 ight)) (3)

Mặt khác trong hình bình hành BB’C’C ta có:

(BC"^2 + B"C^2 = 2left( b^2 + c^2 ight)) (4)

Thay (4) vào (3) ta được :

(AC"^2 + BD"^2 + A"C^2 + B,"D^2 = 4left( a^2 + b^2 + c^2 ight)) (đpcm).

Câu 39 trang 68 SGK Hình học 11 nâng cao

 Cho hình chóp cụt ABC.A’B’C’ tất cả đáy bự ABC cùng các ở kề bên AA’, BB’, CC’. Hotline M, N, p. Lần lượt là trung điểm của những cạnh AB, BC, CA và M’, N’, P’ theo thứ tự là trung điểm của các cạnh A’B’, B’C’, C’A’. Chứng minh MNP.M’N’P’ là hình chóp cụt

• Cửa hàng armani tại việt nam
• Top 10 cầu thủ chạy nhanh nhất thế giới mới nhất 2022
• Học viện bóng đá viettel
• Bảng giá dây điện lõi nhôm