Giải bất phương trình vô tỉ

Dưới đấy là các dạng bất phương trình vô tỉ và gợi ý phương pháp, cách giải những bất phương trình vô tỉ đó. Nhằm cung cấp cho các em những phương thức mạnh duy nhất để giải quyết những bài toán này, shop chúng tôi tổng vừa lòng được tài liệu với những phương thức cực tốt được trình làng ngay bên dưới bài viết này. Hãy cùng chúng tôi xem qua các phương pháp bằng phương pháp tải tài liệu xuống nhé!

TẢI XUỐNG PDF ↓

Kĩ thuật cách xử lý bất phương trình vô tỉ

Phương pháp thay đổi tương đươngKĩ thuật chia điều kiệnKĩ thuật khai cănKĩ thuật đối chiếu thành nhân tửKĩ thuật nhân phân chia liên hợpKĩ thuật để ẩn phụ – Đặt ẩn phụ lượng giácKĩ thuật đánh giá trong bất phương trìnhKĩ thuật sử dụng tích vô vị trí hướng của véc tơ để giải bất phương trìnhKĩ thuật điều tra khảo sát hàm số để review bất phương trình vô tỉKĩ thuật sử dụng tính đối xứng của hai nghiệm

Phương pháp thay đổi tương đương giải bất phương trình

Hai bất phương trình được gọi tương đương khi chúng bao gồm cùng tập nghiệm. Cộng trừ nhị vế của bất phương trình với 1 biểu thức cơ mà không làm chuyển đổi điều kiện của bất phương trình. Nhân phân tách hai vế của bất phương trình với 1 biểu thức luôn dương hoặc âm mà không làm biến đổi điều khiếu nại của bất phương trình. Lũy thừa bậc lẻ nhì vế, khai căn bậc lẻ nhị vế của một bất phương trình. Lũy quá bậc chẵn nhì vế, khai căn bậc chẵn nhì vế khi hai vế của bất phương trình thuộc dương. Nghịch đảo hai vế của bất phương trình khi nhị vế thuộc dương ta đề xuất đổi chiều.

Bạn đang xem: Giải bất phương trình vô tỉ

Kỹ thuật lũy thừa hai vế

Ở kinh nghiệm này, sệt biệt để ý tới đk của bài bác toán. Nếu đk đơn giản có thể kết hợp vào bất phương trình, còn điều kiện phức tạp nên để riêng.

Kỹ thuật khai căn

Biến đổi các biểu thức vào căn thức thành hằng đẳng thức.

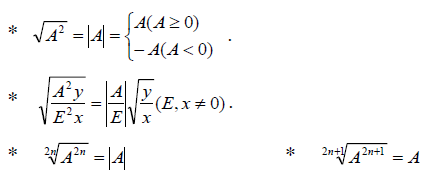
Kỹ thuật phân tích thành nhân tử đem đến bất phương trình tích

Đây là kỹ thuật giải đòi hỏi có tứ duy cao, năng lực phân tích thành nhân tử thành thạo, rất cần phải nhìn ra nhân tử thông thường nhanh.

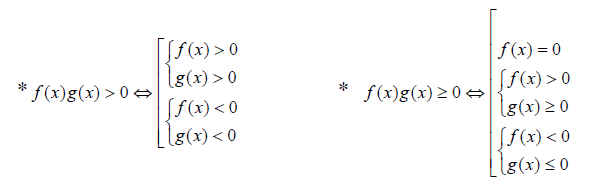
Kỹ thuật nhân chia liên hợp

Nên nhẩm với một số nghiệm nguyên đơn giản.Chú ý tới những biểu thức nhân phân chia liên hợp.

Xem thêm: Cách Làm Trà Sữa Từ Lá Chè Xanh Chuẩn Vị, Cách Làm Trà Sữa Chè Xanh Chuẩn Vị

Phương pháp để ẩn phụ

Một số yêu cầu là: Dạng này học viên cần nhớ giải pháp đặt ẩn cùng từ đó không ngừng mở rộng cho bài toán tương tự chú ý tới các điều khiếu nại của ẩn.

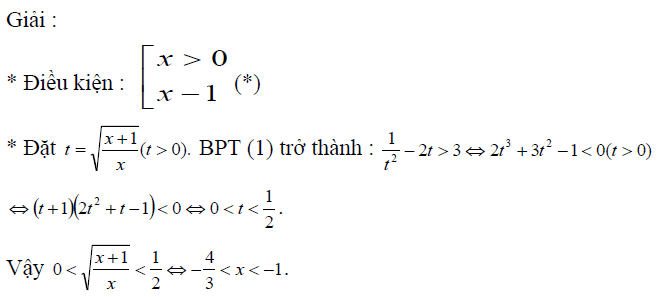
Phương pháp đánh giá bằng bất đẳng thức

– ghi nhớ được bí quyết xét tính solo điệu của một hàm số, lập bảng phát triển thành thiên…– Nhớ những bất đẳng thức.– thường áp dụng cho những Bài toán bất phương trình vô tỉ đặc thù, phức tạp không tồn tại thuật toán rõ ràng nhưnghay có trong những kì thi đại học những năm ngay sát đây. Hai bất đẳng thức cơ bản nhất là:

Bất đẳng thức CôsiBất đẳng thức Bunhiacopski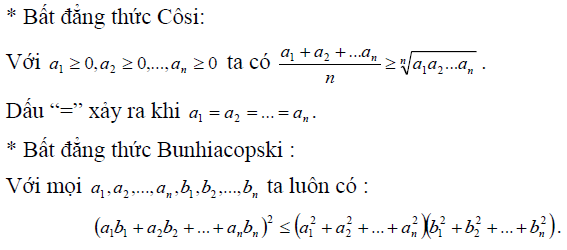

Kỹ thuật thực hiện tích vô vị trí hướng của hai véc tơ trong bất phương trình

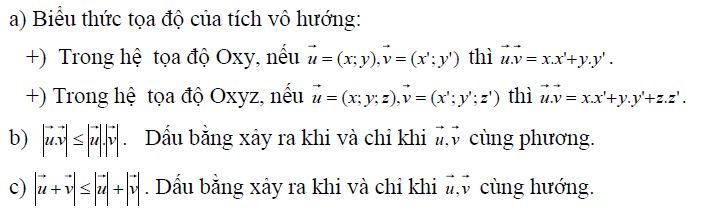
Kỹ thuật khảo sát hàm số để review bất phương trình

Để giải bất phương trình ta điều tra khảo sát hoặc căn cứ vào tính chất của các hàm số đưa ra bảng trở thành thiên cùng từbảng trở thành thiên giới thiệu kết luận.

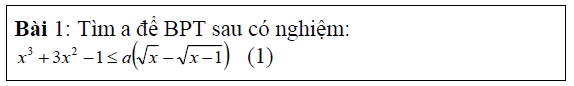
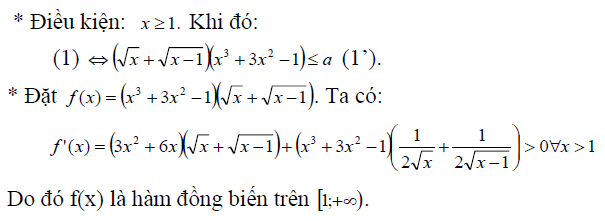
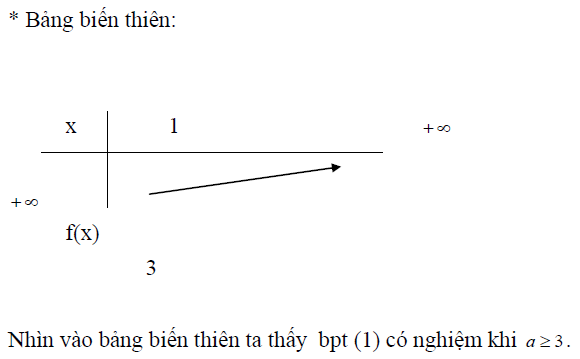
Kỹ thuật sử dụng tính đối xứng của nhì nghiệm

Đây là cách review bất phương trình vô tỉ khá thông minh, các cách làm cho được phụ thuộc kinh nghiệm của bạn giải bài tập. Phụ thuộc mức độ va đụng với những loại bài tập đó.

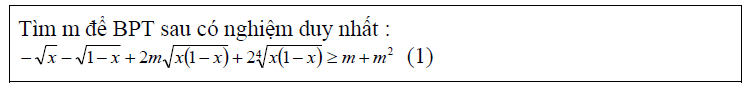
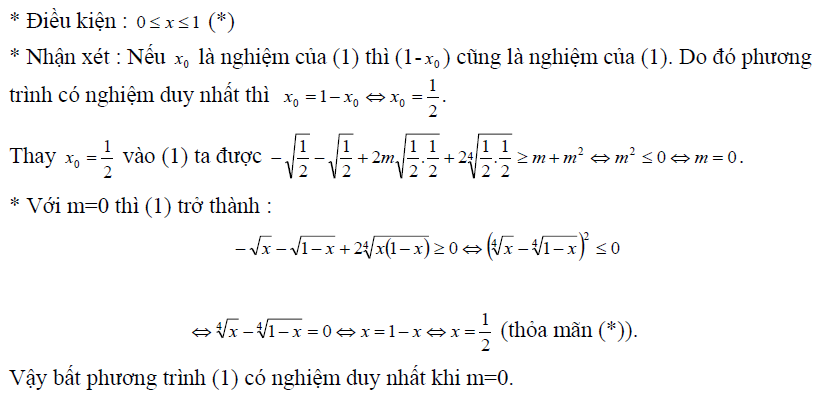
Tổng hợp các bài tập giải bất phương trình vào tài liệu

Dưới đấy là một số bài tập giải bất phương trình vô tỉ bao gồm chọn lọc từ khá nhiều nguồn. Để xem không thiếu thốn lời giải cũng giống như đề bài bác tất cả, các bạn đọc có thể tải file về và in ra nếu đề xuất thiết. Trong khi vẫn còn một trong những bài tập không tồn tại lời giải, bài xích tập đề nghị. Các chúng ta có thể trao đổi ở ngay dưới tài liệu này!

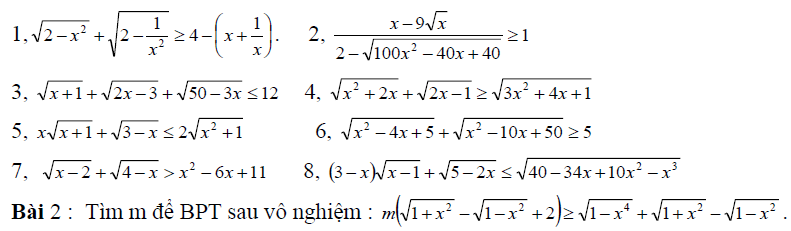
Vậy là chúng ta vừa tham khảo dứt 10 cách thức giải bất phương trình vô tỉ cơ phiên bản nhất, thông dụng nhất. Các phương pháp trên không chỉ là giúp bọn họ giải những bài tập cơ bạn dạng mà còn một vài bài tập trong số đề thi HSG nếu biết cách khai thác.